Οι ασθένειες απασχολούσαν τους ανθρώπους σε όλες τις χρονικές περιόδους. Η ελονοσία και η φυματίωση πιστεύεται ότι ήταν η αιτία για την καταστροφή της Αρχαίας Αιγύπτου πριν από 5.000 χρόνια. Από το 541 έως το 542 μ.Χ η παγκόσμια πανδημία, γνωστή ως η "Πανώλη του Ιουστινιανού" εκτιμάται ότι σκοτωσε το 15-25% του παγκόσμιου πληθυσμού που τότε ήταν περίπου 200 εκατομμύρια . Μετά την ισπανική κατάκτηση του Μεξικού, ο εγγενής πληθυσμός μειώθηκε από περίπου 30 εκατομμύρια το 1519 σε μόλις τρία εκατομμύρια 50 χρόνια αργότερα.
Σήμερα δίνουμε μάχη να ελέγξουμε τον ιό covid-19, ο οποίος είναι πιθανό να προκαλέσει την πιο θανατηφόρα πανδημία στην ανθρώπινη ιστορία.
Στη μάχη για την αντιμετώπιση του συμβάλουν και τα μαθηματικά. Με περίπλοκα μαθηματικά μοντέλα οι ερευνητές μπορούν να προβλέπουν την εξέλιξη των ασθενειών και να κατανοούν την επίδραση των παρεμβάσεων στην εξάπλωση της νόσου. Με πιο πολύπλοκα μοντέλα μπορούμε να απαντήσουμε σε ερωτήσεις σχετικά με τον τρόπο αποτελεσματικής διάθεσης περιορισμένων πόρων ή να υπολογίσουν τις συνέπειες των παρεμβάσεων δημόσιας υγείας, όπως το κλείσιμο καταστημάτων και την απαγόρευση συναντήσεων.
Ένα από τα απλούστερα μαθηματικά μοντέλα για την διάδοση ασθενειών είναι η κατηγοριοποίηση του πληθυσμού σε τρεις ομάδες. Η πρώτη ομάδα αποτελέται απο τους ανθρώπους που χαρακτηρίζονται "suceptible" δηλαδή ευαίσθητοι και είναι οι άνθρωποι που ακόμα δεν έχουν νοσήσει. Ο καθένας θεωρείται ότι γεννιέται ευαίσθητος και είναι δυνατόν να μολυνθεί. Η δεύτερη ομάδα είναι οι άνθρωποι που έχουν μολυνθεί και χαρακτηρίζονται ως μεταδοτικοί "infectives" και η τρίτη ομάδα είναι οι άνθρωποι που έχουν μολυνθεί και έχουν ξεπεράσει την ασθένεια που χαρητολογωντας χαρακτηρίζονται ως "removed" δηλ. που αφαιρούνται. Λόγω των τριών αυτών ομάδων το μοντέλο ονομάζεται S-I-R.
Σκεφτείτε έναν πληθυσμό που είναι suceptible σε μια συγκεκριμένη ασθένεια - όπως ο παγκόσμιος πληθυσμός τον Δεκέμβριο του 2019, στην αρχή της επιδημίας COVID-19. Ο μέσος αριθμός των ατόμων που μολύνονται από έναν μόνο νέο φορέα της ασθένειας είναι γνωστός ως ο βασικός αριθμός αναπαραγωγής Ro. Ο χρόνος που θα διαρκέσει μια επιδημία εξαρτάται σε μεγάλο βαθμό από τον αριθμό αυτό.
Εάν ο αριθμός αυτός είναι μικρότερος από ένα τότε η επιδημία θα έχει σύντομο χρόνο ζωή καθώς κάθε ένας άνθρωπος μολύνει λιγότερο από έναν άλλο άνθρωπο. Αν ο αριθμός αυτός είναι μεγαλύτερος από ένα τότε η αύξηση του αριθμού των κρουσμάτων θα είναι εκθετική.
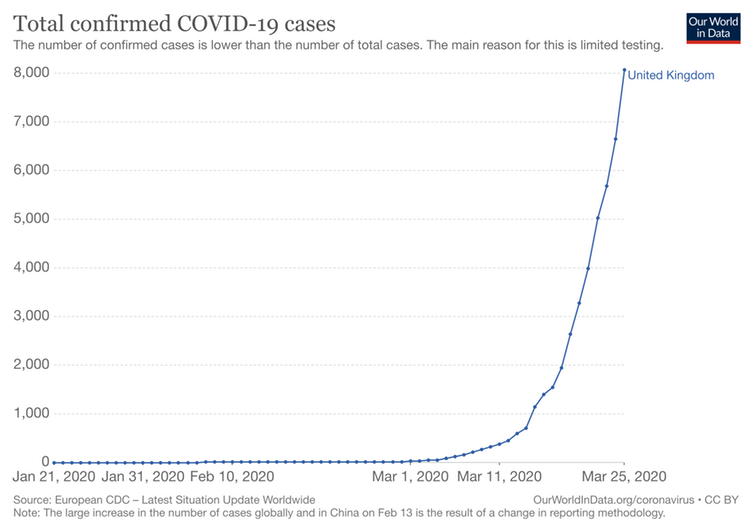
Η εκθετική αύξηση είναι εντυπωσιακή ιδίως στην αρχή της επιδημίας. Εαν υποθέσουμε ότι μετά από 10 φάσεις (σε κάθε φάση ένας μολύνει δύο άλλους) έχουν μολυνθεί 1000 άτομα, δέκα φάσεις μετά θα έχουν μολυνθεί πάνω από ένα εκατομμύριο.
Στην πραγματικότητα βέβαια η εκρηκτική αύξηση δεν μπορεί να διατηρηθεί επ' άπειρον Μετά από κάποιο διάστημα φτάνει σε μία μέγιστη τιμή και στη συνέχεια αρχίζει να μειώνεται. Σε κάθε περίπτωση ένα μέρος του πληθυσμού θα παραμείνει χωρίς να έχει νοσήσει.
Με το μοντέλο αυτό μπορεί να υπολογιστεί ο τελικός αριθμός των ανθρώπων οι οποίοι θα έχουν νοσήσει ή δεν θα έχουν νοσήσει στο τέλος της επιδημίας. Μιλώντας για τον covi-19 αν υποθέσουμε ότι ο αριθμός αναπαραγωγής έχει τη μικρότερη τιμή δηλαδή το 1,5 και χωρίς να παρθούν μέτρα τότε το 58% του πληθυσμού θα μολυνθεί ενώ εάν ο ρυθμός αναπαραγωγής πάρει την ψηλότερη τιμή δηλαδή 4 μόνο το 2% στον πληθυσμό θα μείνει χωρίς να έχει μολυνθεί.
Το ποσοστό θανάτων και ο αριθμός αναπαραγωγής.
Ο αριθμός αναπαραγωγής δεν μπορεί να μας περιγράψει το πόσο σοβαρή είναι η ασθένεια για τον κάθε ασθενή παρόλα αυτά μπορεί να μας δώσει κάποιες ενδείξεις.
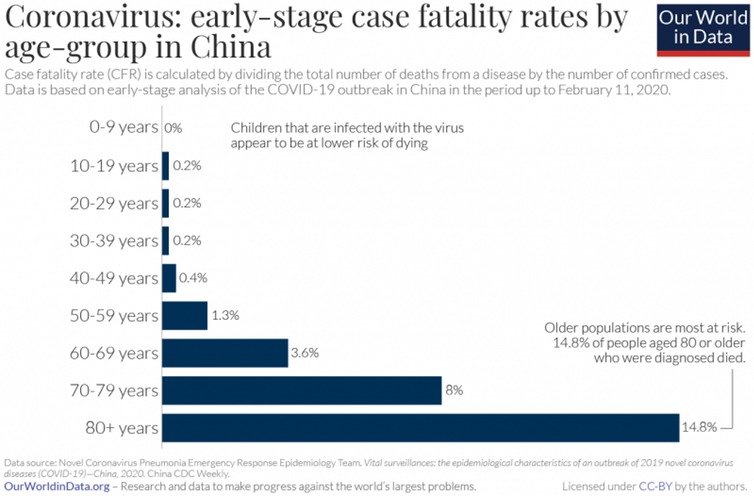
Καθώς για την ιλαρά ο αριθμός αυτός είναι μεταξύ 12 και 18 η συγκεκριμένη ασθένεια έχει πάρα πολύ μικρό ποσοστό θνησιμότητας στον αντίποδα ο Έμπολα με ποσοστό θνησιμότητας 50 έως 70% έχει αριθμό αναπαραγωγής μικρότερο του 1,5. Για τον covid-19 το ποσοστό θνησιμότητας κυμαίνεται μεταξύ από 0,25 έως 3,5% και επηρεάζεται πάρα πολύ από την ηλικιακή κατανομή.
Είναι σημαντικό να αντιληφθούμε ότι για το συνολικό αριθμό των θυμάτων ο αριθμός αναπαραγωγής είναι πιο σημαντικός από το ποσοστό θνησιμότητας. Αυτό γίνεται φανερό από την περίπτωση του Έμπολα που σε σύγκριση με τον covi-19 προκαλεί πολύ λιγότερους θανάτους ενώ έχει πολύ μεγαλύτερο ποσοστό θνησιμότητας.
Αλλά ο εμβολιασμός είναι προληπτικό μέτρο που χρησιμοποιείται για να μειώσει την πιθανότητα εμφάνισης κρουσμάτων. Στην περίπτωση της πανδημίας του covid- 19 για τον οποίο δεν υπήρχαν εμβόλια απαιτείται ένα εύλογο χρονικό διάστημα για να δημιουργηθεί.
Η καραντίνα και απομόνωση είναι αποτελεσματικές στη μείωση του ρυθμού μετάδοσης καθώς μειώνουν τον πραγματικό αριθμό αναπαραγωγής. Οι άνθρωποι οι οποίοι νοσούν εάν απομονωθούν δεν μεταδίδουν στους υγιείς και έτσι ο πραγματικός αριθμός αναπαραγωγής μειώνεται.
Η κοινωνική απόσταση (social distancing) καθώς και η αυτό-απομόνωση (self-isolation) είναι δύο σημαντικά μέτρα τα οποία μπορούν να μειώσουν τον αριθμό αναπαραγωγής και να εμποδίσουν την εξάπλωση του covid-19.
Το ποσοστό των ανθρώπων οι οποίοι θα πρέπει να είναι να έχουν ανοσία για να δημιουργηθεί η ανοσία της αγέλης και να προστατεύσουν και τους υπόλοιπους εξαρτάται από το πόσο μεταδοτική είναι η ασθένεια. Εάν ο βασικός αριθμός αναπαραγωγής είναι μεγάλος τόσο μεγαλύτερο θα πρέπει να είναι και το ποσοστό του πληθυσμού το οποίο θα πρέπει να νοσήσει. Για να δημιουργηθεί η ανοσία της αγέλης αν για παράδειγμα μία ασθένεια έχει αριθμό αναπαραγωγής 4 το μοντέλο S-I-R προβλέπει ότι τα θα πρέπει να νοσήσουν τα 3/4 του πληθυσμού δηλαδή στην περίπτωση της Ελλάδας επτάμισι εκατομμύρια άνθρωποι. Αν ο αριθμός αυτός είναι στο 1,5 τότε πιθανώς μόνο το ένα τρίτο του πληθυσμού πρέπει να αποκτήσει ανοσία για να προστατεύσει τα υπόλοιπα.
Στην περίπτωση που βρεθεί ένα εμβόλιο τότε η ανοσία της αγέλης μπορεί να επιτευχθεί με εμβολιασμό ικανοποιητικού αριθμού ανθρώπων. Χωρίς όμως αυτό όπως στην περίπτωση του covid- 19 ο μόνος τρόπος για να αποκτηθεί η ανοσία της αγέλης είναι οι άνθρωποι να νοσήσουν. Με βάση τα ποσοστά θνησιμότητας αυτό θα συνεπαγόταν το θάνατο πολλών χιλιάδων ανθρώπων.
Ιδίως στην περίπτωση του covid-19 που τα δεδομένα προκύπτουν τώρα. Ενα πρόβλημα που υπάρχει με το νέο κορονοϊό είναι η ασυμπτωματική περίοδος κατά την έναρξη της νόσου στη διάρκεια της οποίας οι άνθρωποι μπορούν να έχουν τον ιό και να μολύνουν χωρίς να παρουσιάζουν οι ίδιοι συμπτώματα αυτό σημαίνει ότι πρέπει να προσθέσουμε μία κατηγορία ανθρώπους στο μοντέλο S-I-R Είναι οι άνθρωποι που έχουν μολυνθεί είναι ικανοί να μεταδώσουν την ασθένεια ενώ δεν εμφανίζουν συμπτώματα και είναι η λεγόμενη κατηγορία "carrier" (φορέας). Αυτό αλλάζει το μοντέλο από S-I-R σε S-C-I-R. Ένα τέτοιο μοντέλο χρησιμοποιείται και στην περίπτωση του HIV/AIDS.
Σήμερα οι κυβερνήσεις για τη χάραξη πολιτικής χρησιμοποιούν μοντέλα ακόμα πιο περίπλοκα δυστυχώς όμως ακόμα και αυτά τα περίπλοκα μοντέλα είναι δύσκολο να προβλέψουν πότε η σημερινή πανδημία θα φτάσει στο τέρμα της.
Το κείμενο γράφτηκε με βάση το 'Modeling a Pandemic: How R0 And SIR Can Help Control An Outbreak" που δημοσιεύθηκε στοscience20.org
Σήμερα δίνουμε μάχη να ελέγξουμε τον ιό covid-19, ο οποίος είναι πιθανό να προκαλέσει την πιο θανατηφόρα πανδημία στην ανθρώπινη ιστορία.
Στη μάχη για την αντιμετώπιση του συμβάλουν και τα μαθηματικά. Με περίπλοκα μαθηματικά μοντέλα οι ερευνητές μπορούν να προβλέπουν την εξέλιξη των ασθενειών και να κατανοούν την επίδραση των παρεμβάσεων στην εξάπλωση της νόσου. Με πιο πολύπλοκα μοντέλα μπορούμε να απαντήσουμε σε ερωτήσεις σχετικά με τον τρόπο αποτελεσματικής διάθεσης περιορισμένων πόρων ή να υπολογίσουν τις συνέπειες των παρεμβάσεων δημόσιας υγείας, όπως το κλείσιμο καταστημάτων και την απαγόρευση συναντήσεων.
Το μοντέλο S-I-R
Ένα από τα απλούστερα μαθηματικά μοντέλα για την διάδοση ασθενειών είναι η κατηγοριοποίηση του πληθυσμού σε τρεις ομάδες. Η πρώτη ομάδα αποτελέται απο τους ανθρώπους που χαρακτηρίζονται "suceptible" δηλαδή ευαίσθητοι και είναι οι άνθρωποι που ακόμα δεν έχουν νοσήσει. Ο καθένας θεωρείται ότι γεννιέται ευαίσθητος και είναι δυνατόν να μολυνθεί. Η δεύτερη ομάδα είναι οι άνθρωποι που έχουν μολυνθεί και χαρακτηρίζονται ως μεταδοτικοί "infectives" και η τρίτη ομάδα είναι οι άνθρωποι που έχουν μολυνθεί και έχουν ξεπεράσει την ασθένεια που χαρητολογωντας χαρακτηρίζονται ως "removed" δηλ. που αφαιρούνται. Λόγω των τριών αυτών ομάδων το μοντέλο ονομάζεται S-I-R.
Σκεφτείτε έναν πληθυσμό που είναι suceptible σε μια συγκεκριμένη ασθένεια - όπως ο παγκόσμιος πληθυσμός τον Δεκέμβριο του 2019, στην αρχή της επιδημίας COVID-19. Ο μέσος αριθμός των ατόμων που μολύνονται από έναν μόνο νέο φορέα της ασθένειας είναι γνωστός ως ο βασικός αριθμός αναπαραγωγής Ro. Ο χρόνος που θα διαρκέσει μια επιδημία εξαρτάται σε μεγάλο βαθμό από τον αριθμό αυτό.
Εάν ο αριθμός αυτός είναι μικρότερος από ένα τότε η επιδημία θα έχει σύντομο χρόνο ζωή καθώς κάθε ένας άνθρωπος μολύνει λιγότερο από έναν άλλο άνθρωπο. Αν ο αριθμός αυτός είναι μεγαλύτερος από ένα τότε η αύξηση του αριθμού των κρουσμάτων θα είναι εκθετική.
Η εκθετική αύξηση των κρουσμάτων
Οι πρώτες εκτιμήσεις σε σχέση με τον covid-19 τοποθετούν τον αριθμό αυτό μεταξύ 1,5 και 4. Το Δεκέμβριο και τον Ιανουάριο η τιμή αυτή ήταν τουλάχιστον 2 που σημαίνει ότι κάθε ένας που νοσούσε μετέδιδε την ασθένεια τουλάχιστον σε δύο άλλους που με τη σειρά τους κάθε ένας από αυτούς σε δύο άλλους και ούτω καθεξής.Η εκθετική αύξηση είναι εντυπωσιακή ιδίως στην αρχή της επιδημίας. Εαν υποθέσουμε ότι μετά από 10 φάσεις (σε κάθε φάση ένας μολύνει δύο άλλους) έχουν μολυνθεί 1000 άτομα, δέκα φάσεις μετά θα έχουν μολυνθεί πάνω από ένα εκατομμύριο.
Στην πραγματικότητα βέβαια η εκρηκτική αύξηση δεν μπορεί να διατηρηθεί επ' άπειρον Μετά από κάποιο διάστημα φτάνει σε μία μέγιστη τιμή και στη συνέχεια αρχίζει να μειώνεται. Σε κάθε περίπτωση ένα μέρος του πληθυσμού θα παραμείνει χωρίς να έχει νοσήσει.

Με το μοντέλο αυτό μπορεί να υπολογιστεί ο τελικός αριθμός των ανθρώπων οι οποίοι θα έχουν νοσήσει ή δεν θα έχουν νοσήσει στο τέλος της επιδημίας. Μιλώντας για τον covi-19 αν υποθέσουμε ότι ο αριθμός αναπαραγωγής έχει τη μικρότερη τιμή δηλαδή το 1,5 και χωρίς να παρθούν μέτρα τότε το 58% του πληθυσμού θα μολυνθεί ενώ εάν ο ρυθμός αναπαραγωγής πάρει την ψηλότερη τιμή δηλαδή 4 μόνο το 2% στον πληθυσμό θα μείνει χωρίς να έχει μολυνθεί.
Το ποσοστό θανάτων και ο αριθμός αναπαραγωγής.
Ο αριθμός αναπαραγωγής δεν μπορεί να μας περιγράψει το πόσο σοβαρή είναι η ασθένεια για τον κάθε ασθενή παρόλα αυτά μπορεί να μας δώσει κάποιες ενδείξεις.
Καθώς για την ιλαρά ο αριθμός αυτός είναι μεταξύ 12 και 18 η συγκεκριμένη ασθένεια έχει πάρα πολύ μικρό ποσοστό θνησιμότητας στον αντίποδα ο Έμπολα με ποσοστό θνησιμότητας 50 έως 70% έχει αριθμό αναπαραγωγής μικρότερο του 1,5. Για τον covid-19 το ποσοστό θνησιμότητας κυμαίνεται μεταξύ από 0,25 έως 3,5% και επηρεάζεται πάρα πολύ από την ηλικιακή κατανομή.

Είναι σημαντικό να αντιληφθούμε ότι για το συνολικό αριθμό των θυμάτων ο αριθμός αναπαραγωγής είναι πιο σημαντικός από το ποσοστό θνησιμότητας. Αυτό γίνεται φανερό από την περίπτωση του Έμπολα που σε σύγκριση με τον covi-19 προκαλεί πολύ λιγότερους θανάτους ενώ έχει πολύ μεγαλύτερο ποσοστό θνησιμότητας.
Περιορίζοντας μια επιδημία
O πιο σημαντικός και αποτελεσματικός παράγοντας για τη μείωση της εξάπλωσης μιας επιδημίας είναι τα εμβόλια. Με τα εμβόλια οι άνθρωποι οι οποίοι ανήκουν στην κατηγορία "S" (ευαίσθητη) μεταφέρονται απευθείας στην κατηγορία όσων έχουν ανοσία "R" χωρίς να νοσήσουν.Αλλά ο εμβολιασμός είναι προληπτικό μέτρο που χρησιμοποιείται για να μειώσει την πιθανότητα εμφάνισης κρουσμάτων. Στην περίπτωση της πανδημίας του covid- 19 για τον οποίο δεν υπήρχαν εμβόλια απαιτείται ένα εύλογο χρονικό διάστημα για να δημιουργηθεί.
Η καραντίνα και απομόνωση είναι αποτελεσματικές στη μείωση του ρυθμού μετάδοσης καθώς μειώνουν τον πραγματικό αριθμό αναπαραγωγής. Οι άνθρωποι οι οποίοι νοσούν εάν απομονωθούν δεν μεταδίδουν στους υγιείς και έτσι ο πραγματικός αριθμός αναπαραγωγής μειώνεται.
Η κοινωνική απόσταση (social distancing) καθώς και η αυτό-απομόνωση (self-isolation) είναι δύο σημαντικά μέτρα τα οποία μπορούν να μειώσουν τον αριθμό αναπαραγωγής και να εμποδίσουν την εξάπλωση του covid-19.
Ανοσία αγέλης
Η ανοσία της αγέλης, μία ιδέα την οποία φάνηκε να εφαρμόζει αρχικά η μεγάλη Βρετανία, βασίζεται στο ότι αν ένας μεγάλος αριθμός νοσήσει τότε θα σταματήσει η εξάπλωση της επιδημίας. Το πρόβλημα σε αυτή τη στρατηγική βέβαια είναι που ανήκουν στις ευπαθείς ομάδες όπως οι άνθρωποι οι οποίοι είναι ανοσοκατασταλμένοι οι ηλικιωμένοι οι έγκυες γυναίκες και γενικότερα τα άτομα με υποκείμενα νοσήματα.Το ποσοστό των ανθρώπων οι οποίοι θα πρέπει να είναι να έχουν ανοσία για να δημιουργηθεί η ανοσία της αγέλης και να προστατεύσουν και τους υπόλοιπους εξαρτάται από το πόσο μεταδοτική είναι η ασθένεια. Εάν ο βασικός αριθμός αναπαραγωγής είναι μεγάλος τόσο μεγαλύτερο θα πρέπει να είναι και το ποσοστό του πληθυσμού το οποίο θα πρέπει να νοσήσει. Για να δημιουργηθεί η ανοσία της αγέλης αν για παράδειγμα μία ασθένεια έχει αριθμό αναπαραγωγής 4 το μοντέλο S-I-R προβλέπει ότι τα θα πρέπει να νοσήσουν τα 3/4 του πληθυσμού δηλαδή στην περίπτωση της Ελλάδας επτάμισι εκατομμύρια άνθρωποι. Αν ο αριθμός αυτός είναι στο 1,5 τότε πιθανώς μόνο το ένα τρίτο του πληθυσμού πρέπει να αποκτήσει ανοσία για να προστατεύσει τα υπόλοιπα.
Στην περίπτωση που βρεθεί ένα εμβόλιο τότε η ανοσία της αγέλης μπορεί να επιτευχθεί με εμβολιασμό ικανοποιητικού αριθμού ανθρώπων. Χωρίς όμως αυτό όπως στην περίπτωση του covid- 19 ο μόνος τρόπος για να αποκτηθεί η ανοσία της αγέλης είναι οι άνθρωποι να νοσήσουν. Με βάση τα ποσοστά θνησιμότητας αυτό θα συνεπαγόταν το θάνατο πολλών χιλιάδων ανθρώπων.
Τα μοντέλα διαρκώς βελτιώνονται
Στην πραγματικότητα το μοντέλο αυτό δεν είναι αρκετά περίπλοκο έτσι ώστε να μπορεί να προβλέψει όλες τις παραμέτρους.Ιδίως στην περίπτωση του covid-19 που τα δεδομένα προκύπτουν τώρα. Ενα πρόβλημα που υπάρχει με το νέο κορονοϊό είναι η ασυμπτωματική περίοδος κατά την έναρξη της νόσου στη διάρκεια της οποίας οι άνθρωποι μπορούν να έχουν τον ιό και να μολύνουν χωρίς να παρουσιάζουν οι ίδιοι συμπτώματα αυτό σημαίνει ότι πρέπει να προσθέσουμε μία κατηγορία ανθρώπους στο μοντέλο S-I-R Είναι οι άνθρωποι που έχουν μολυνθεί είναι ικανοί να μεταδώσουν την ασθένεια ενώ δεν εμφανίζουν συμπτώματα και είναι η λεγόμενη κατηγορία "carrier" (φορέας). Αυτό αλλάζει το μοντέλο από S-I-R σε S-C-I-R. Ένα τέτοιο μοντέλο χρησιμοποιείται και στην περίπτωση του HIV/AIDS.
Σήμερα οι κυβερνήσεις για τη χάραξη πολιτικής χρησιμοποιούν μοντέλα ακόμα πιο περίπλοκα δυστυχώς όμως ακόμα και αυτά τα περίπλοκα μοντέλα είναι δύσκολο να προβλέψουν πότε η σημερινή πανδημία θα φτάσει στο τέρμα της.
Το κείμενο γράφτηκε με βάση το 'Modeling a Pandemic: How R0 And SIR Can Help Control An Outbreak" που δημοσιεύθηκε στοscience20.org

